Explain the Main Differences Between Definite and Indefinite Integral Calculus
Integration is the reverse of differentiation. The indefinite integral is by definition the primitive of a function or its antiderivative hence it is related by definition to the concept of derivative.

Fundamental Thereom Of Calculus Explained Part 1 2 Examples Definite Integral Youtube
Be sure to include.

. It means the independent variable will not have any given interval. Integrals are also involved in biology. The reason for this will be apparent eventually.
Why differentiate in reverse. Definite integrals aways return a real number after evaluation at its limits of integration OD. In definite integrals the integration gives a finite number.
The definite integral is defined to be exactly the limit and summation that we looked at in the last section to find the net area between a function and the x-axis. An indetinte integral cannot always be integrated analytically and may require numeric integration while it is always possible to integrate a definite integral Definite integrals always return a real number atter evaluation at its limits of integration Oc. Differentiation and Integration are two building blocks.
An indefinite integral cannot always be integrated analytically and may require numerio integration while it is always possible to integrate a definite integral. It is also called as the antiderivative. However the main difference between both the terms is the definite integral in its existence is a real number value while on the other hand antiderivative has an unlimited.
If f is the derivative of F then F is an antiderivative of f. In calculus differentiation is the process by which rate of change of a curve is determined. Keep going and youll find out.
We also call F the indefinite integral of f. Intpi2_0 cos 1 These are distinct concepts. With an indefinite integral there are no upper and lower limits on the integral here and what well get is an answer that still has xs in it and will also have a K plus K in it.
For any function ƒ which is not necessarily non-negative and defined on the interval ab a b ƒ x dx is called the definite integral ƒ on ab. Also note that the notation for the definite integral is very similar to the notation for an indefinite integral. An integral is used to define these two things because integration is the opposite of differentiation.
Later in this chapter we examine how these concepts are related. A definite integral results in a set of. Calculus questions and answers.
A definite integral has upper and lower limits on the integrals and its called definite because at the end of the problem we have a number - it is a definite answer. A definite integral results in a set of. Section 15 Indefinite Integrals In this section we focus on the indefinite integral.
Definite integrals always return a real number after evaluation at its limits of integration. Be sure to include what form the answers to each integral take function number etc and what the answers mean. In other words indefinite integrals and antiderivatives are essentially reverse derivatives.
Its definition the differences between the definite and indefinite integrals some basic integral rules and how to compute a definite integral. Explain the difference between an indefinite integral and a definite integral. 1st we will get an equation for our answer rather than a value.
An indefinte integral cannot always be integrated analytically and may require numeric integration while it is always possible to integrate a definite integral. But by custom we use the same symbol for them because the Fundamental Theorem of Calculus tells us that. In this section aspirants will learn about the indefinite and definite Integration list of important formulas how to use integral properties to solve integration problems integration methods and many more.
An indefinite integral is also defined and continuous over the interval of integration but may have to as a limit of integration OB. It sums up all small area lying under a curve and finds out the total area. No relation a priori with the derivatives.
So the two integrals are independently defined concepts. Indefinite integrals associate an arbitrary variable hence the family of functions and definite integrals do not have an arbitrary constant but an upper limit and a lower limit of integration. Since the indefinite integral doesnt have bounds two things will be different from calculating a definite integral.
Now what I want to do in this video is connect the first fundamental theorem of calculus to the second part or the second fundamental theorem of calculus which we tend to use to actually evaluate definite integrals. Also in this section we are introduced to some new integrals. An indefinite integral after evaluating it at the limits of integration results in a particular number.
And yes I do explain all of this very clearly and repeatedly to my students The definite integral or area function of cos from 0 to pi2 is 1. So lets think about what F of b minus F of a is what this is where both b and a are also in this interval. You can find the Indefinite Integrals and Definite Integrals values with the help of online tools like definite integral calculator and indefinite integral calculator.
6 rows The main difference between Definite and Indefinite Integral is that a definite integral. A definite integral is defined and continuous over the interval of integration and has finite limits of integration. An indefinite integral is a family of functions.
The indefinite integrals are not bounded from both the endpoints. A definite integral is a number. The definite integral is by definition a limit of a certain class of sums the class of the Riemann sums by the way.
Likewise you would determine velocity by using the indefinite integral of acceleration a EDT. If ƒ x F x then ƒ x dx F xC where C is a constant ƒ x dx is called the indefinite integral of ƒ x. However close attention should always be paid to notation so we know whether were working with a definite integral or an indefinite integral.
A definite integral is defined and continuous over the interval of integration and has finito limits of integration An indefinite. An indefinite integral after evaluating it at the limits of integration results in a particular number. 2nd we need to add a c to all of our equations.
Difference between Differentiation and Integration. An indefinite integral after evaluating it at the limits of integration fosults in a particular number. Integration is just the opposite of differentiation.
Consequently to find displacement you would use the indefinite integral of velocity v EDT. Explain the difference between an indefinite integral and a definite integral. Subsection 151 Defining the Indefinite Integral.
The indefinite integral is defined as a function that will describe an area. But for definite integration both endpoints are specific and definite.

Pdf Definitions And Images For The Definite Integral Concept

Calculus Antiderivatives And The Indefinite Integral Mathematics Stack Exchange

Calculus Definite Integrals Youtube

Calculus Ii Chapter 5 Definite Integral Example Ppt Download

Lesson Explainer The Fundamental Theorem Of Calculus Evaluating Definite Integrals Nagwa

Introduction To Definite Integrals

Calculus Lesson 16 Indefinite And Definite Integrals Don T Memorise Youtube

Ap Calculus Exam Review Integrals Magoosh Blog High School

What S The Difference Between A Definite Integral And An Indefinite Integral Calculus Youtube
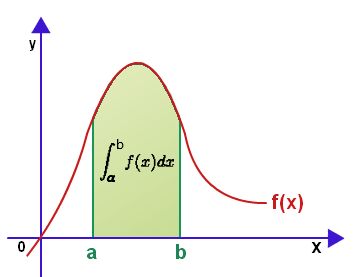
What Is The Difference Between A Definite And Indefinite Integral Socratic

Calculus Change Of Variables For Definite Integrals Mathematics Stack Exchange

Computing Indefinite Integrals

Definite Integral Properties And Proofs Protonstalk

Definite Integral Calculus Examples Integration Basic Introduction Practice Problems Youtube

How To Calculate A Definite Integral Using A Combination Of Areas And Properties Of Definite Integrals Calculus Study Com

Solved Explain The Difference Between An Indefinite Integral Chegg Com



Comments
Post a Comment